演讲者:Michael Röckner(比勒费尔德大学)
时间:2017-10-19 08:35-09:30
地点:慧园3栋 415报告厅
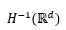 is proved for the stochastic nonlinear FokkerPlanck
equation
is proved for the stochastic nonlinear FokkerPlanck
equation 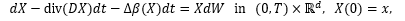 ,
via a corresponding random differential equation. Here d ≥ 1, W is a Wiener process in
,
via a corresponding random differential equation. Here d ≥ 1, W is a Wiener process in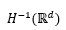
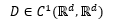 and β is a continuous monotonically increasing function satisfying
some appropriate polynomial growth conditions. The solution exists for
and β is a continuous monotonically increasing function satisfying
some appropriate polynomial growth conditions. The solution exists for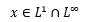 and
preserves positivity. If β is locally Lipschitz, the solution is unique, path-wise Lipschitz continuous
with respect to initial data in
and
preserves positivity. If β is locally Lipschitz, the solution is unique, path-wise Lipschitz continuous
with respect to initial data in . Stochastic Fokker-Planck equations with nonlinear
drift of the form
. Stochastic Fokker-Planck equations with nonlinear
drift of the form 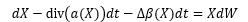 are also considered for Lipschitzian
continuous functions
are also considered for Lipschitzian
continuous functions 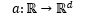 .
Joint work with Viorel Barbu (Romanian Academy of Sciences, Iasi).
.
Joint work with Viorel Barbu (Romanian Academy of Sciences, Iasi).